Chapter 6 Beschrijvende statistieken
In dit hoofdstuk maken we weer gebruik van de mpg data en het tidyverse package.
6.1 Descriptieven
Met descriptieven worden verschillende statistische maten, zoals het gemiddelde en de standaarddeviatie, bedoeld. De beschrijvende maten kunnen via de volgende commando’s verkregen worden.
mean();gemiddeldemedian();mediaansd();standaarddeviatiemin();laagste scoremax();hoogste scoreIQR();interkwartielafstand
let op: vaak als er een foutmelding komt bij het gebruiken van deze functies en de uitkomst NA is, komt dit doordat er nog missende waarden zijn bij de variabele die je wilt gebruiken.
De zogenoemde vijf-nummer-samenvatting, of te wel het minimum, de kwartielen en het maximum, kan ook verkregen worden via summary().
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.600 2.400 3.300 3.472 4.600 7.000Deze informatie kan ook snel opgevraagd worden met de code skim(), hierbij wordt er ook een overzicht gegeven van de verdeling van alle variabelen in de dataset. Deze code is onderdeel van het skimr- package.
6.2 Frequentietabellen
Een frequentietabel geeft een beknopt overzicht van de verdeling van een variabele. Een frequentietabel kan gemaakt worden met table().
##
## 2seater compact midsize minivan pickup subcompact suv
## 5 47 41 11 33 35 62Door een tweede variabele toe te voegen, wordt er een extra laag toegvoegd aan de tabel.
##
## 2seater compact midsize minivan pickup subcompact suv
## 4 0 12 3 0 33 4 51
## f 0 35 38 11 0 22 0
## r 5 0 0 0 0 9 11Soms is het nuttig om ook de missende waarde zichtbaar te krijgen in de frequentietabel, dit kan met de toevoeging useNA = "always".
##
## 2seater compact midsize minivan pickup subcompact suv
## 5 47 41 11 33 35 62
## <NA>
## 0In tidyverse zit ook een manier om een frequentietabel te maken. Deze kan handig zijn wanneer je gebruik wilt maken van een filter of een groepsindeling. Tidyverse heeft daar overzichtelijkere tools voor dan Base R, maar vereist wel het gebruik van andere code, namelijk count().
## # A tibble: 38 × 2
## model n
## <chr> <int>
## 1 4runner 4wd 6
## 2 a4 7
## 3 a4 quattro 8
## 4 a6 quattro 3
## 5 altima 6
## 6 c1500 suburban 2wd 5
## 7 camry 7
## 8 camry solara 7
## 9 caravan 2wd 11
## 10 civic 9
## # ℹ 28 more rowsDe frequentietabel die je dan produceert is een tibble, waarvan je soms niet meteen alle rijen kunt zien. Je kunt hiervoor ook de print (n = ...) functie gebruiken, met behulp van een pipe.
## # A tibble: 38 × 2
## model n
## <chr> <int>
## 1 4runner 4wd 6
## 2 a4 7
## 3 a4 quattro 8
## 4 a6 quattro 3
## 5 altima 6
## 6 c1500 suburban 2wd 5
## 7 camry 7
## 8 camry solara 7
## 9 caravan 2wd 11
## 10 civic 9
## 11 corolla 5
## 12 corvette 5
## 13 dakota pickup 4wd 9
## 14 durango 4wd 7
## 15 expedition 2wd 3
## 16 explorer 4wd 6
## 17 f150 pickup 4wd 7
## 18 forester awd 6
## 19 grand cherokee 4wd 8
## 20 grand prix 5
## 21 gti 5
## 22 impreza awd 8
## 23 jetta 9
## 24 k1500 tahoe 4wd 4
## 25 land cruiser wagon 4wd 2
## 26 malibu 5
## 27 maxima 3
## 28 mountaineer 4wd 4
## 29 mustang 9
## 30 navigator 2wd 3
## 31 new beetle 6
## 32 passat 7
## 33 pathfinder 4wd 4
## 34 ram 1500 pickup 4wd 10
## 35 range rover 4
## 36 sonata 7
## 37 tiburon 7
## 38 toyota tacoma 4wd 7Er is ook een mogelijkheid om aan te geven of de cellen van de frequentietabel die leeg zijn gebleven, weergeven moeten worden. Dit doe je door de volgende toevoeging .drop= FALSE. Deze code werkt alleen met factoren.
Proporties
Met de code prop.table(table()) wordt de verdeling van de variable in proporties weergeven.
##
## 2seater compact midsize minivan pickup subcompact suv
## 0.02136752 0.20085470 0.17521368 0.04700855 0.14102564 0.14957265 0.26495726Ook hier kan een tweede variabele toegvoegd worden. Daarbij kan aangegeven worden of de rij of de kolomproporties getoond moeten worden: 1 = rijpercentage, 2 = kolompercentage.
##
## 4 f r
## 2seater 0.00000000 0.00000000 1.00000000
## compact 0.25531915 0.74468085 0.00000000
## midsize 0.07317073 0.92682927 0.00000000
## minivan 0.00000000 1.00000000 0.00000000
## pickup 1.00000000 0.00000000 0.00000000
## subcompact 0.11428571 0.62857143 0.25714286
## suv 0.82258065 0.00000000 0.17741935##
## 4 f r
## 2seater 0.00000000 0.00000000 0.20000000
## compact 0.11650485 0.33018868 0.00000000
## midsize 0.02912621 0.35849057 0.00000000
## minivan 0.00000000 0.10377358 0.00000000
## pickup 0.32038835 0.00000000 0.00000000
## subcompact 0.03883495 0.20754717 0.36000000
## suv 0.49514563 0.00000000 0.44000000Cumulatieve proporties
Het maken van een frequentietabel met cumulatieve proporties kan met behulp van de code mutate(). De mutate() functie kan met behulp van pipes toegevoegd worden aan de count() functie.
## # A tibble: 3 × 3
## drv n cumulatief
## <fct> <int> <dbl>
## 1 4 103 0.440
## 2 f 106 0.893
## 3 r 25 1De naam ‘cumulatief’, kun je zelf veranderen. Het resultaat is een extra kolom in je frequentietabel, waarbij het cumulatieve percentage staat aangegeven.
Een tweede optie voor het maken van een tabel met cumulatieve frequenties, is via een functie in het epiDisplay- package. De cumulatieve proporties kunnen via de code tab1() opgevraagd worden. Via sort.group kan de volgorde van de informatie aangepast worden.
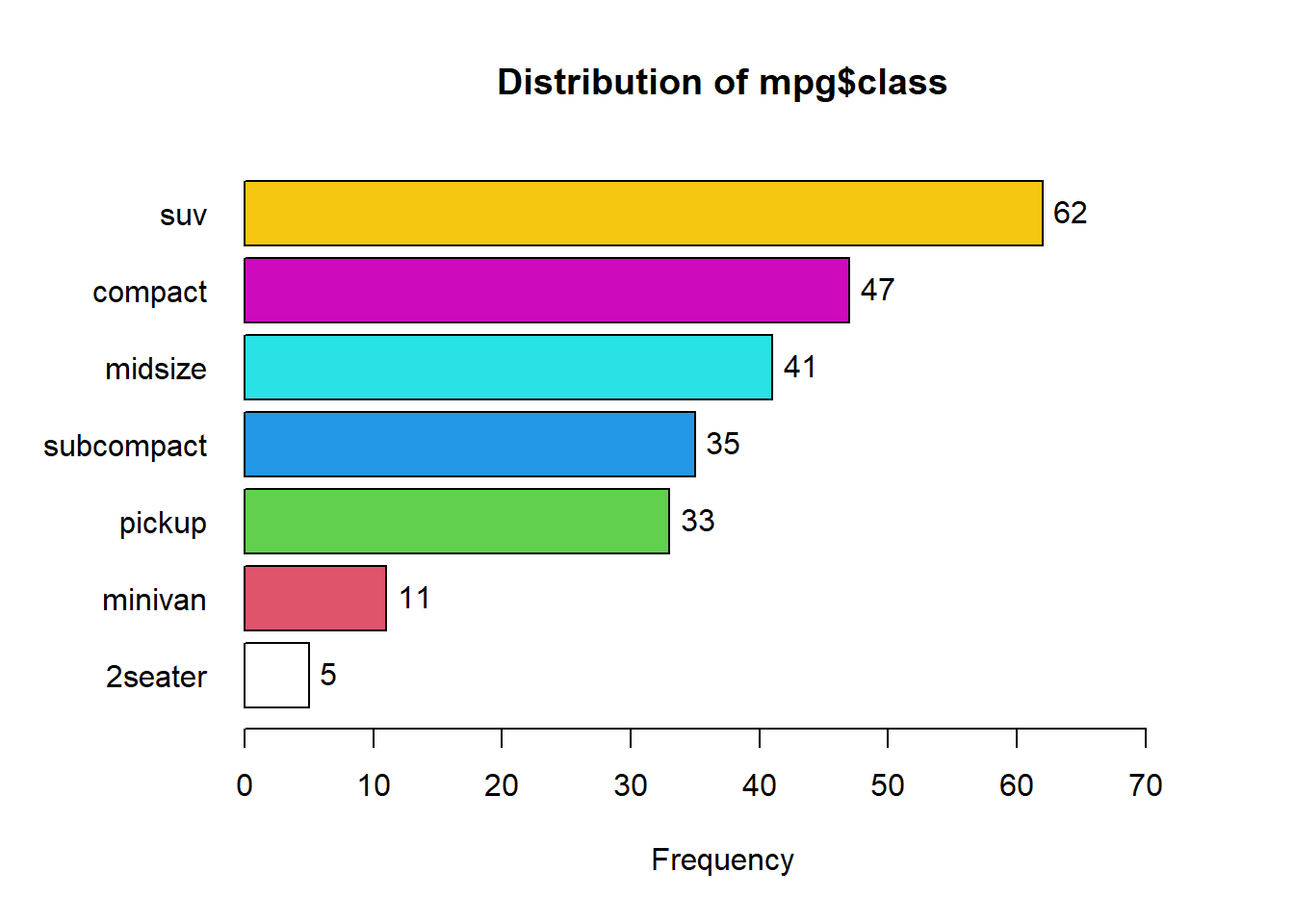
## mpg$class :
## Frequency Percent Cum. percent
## suv 62 26.5 26.5
## compact 47 20.1 46.6
## midsize 41 17.5 64.1
## subcompact 35 15.0 79.1
## pickup 33 14.1 93.2
## minivan 11 4.7 97.9
## 2seater 5 2.1 100.0
## Total 234 100.0 100.06.3 Kruistabel
In een kruistabel worden twee of meer verschillende variabelen met discrete waarden (categorieën) tegen elkaar afgezet. Op deze manier kan gekeken worden hoe vaak de combinaties van waarden op beide variabelen voorkomen, de verdelingen van de variabelen kunnen onderzocht worden (gezamenlijke, conditionele en marginale verdelingen), en de samenhang tussen de twee variabelen kan geïnspecteerd worden. Voor het maken van een kruistabel is het gmodels-package nodig.
##
##
## Cell Contents
## |-------------------------|
## | N |
## | Chi-square contribution |
## | N / Row Total |
## | N / Col Total |
## | N / Table Total |
## |-------------------------|
##
##
## Total Observations in Table: 234
##
##
## | mpg$drv
## mpg$class | 4 | f | r | Row Total |
## -------------|-----------|-----------|-----------|-----------|
## 2seater | 0 | 0 | 5 | 5 |
## | 2.201 | 2.265 | 37.334 | |
## | 0.000 | 0.000 | 1.000 | 0.021 |
## | 0.000 | 0.000 | 0.200 | |
## | 0.000 | 0.000 | 0.021 | |
## -------------|-----------|-----------|-----------|-----------|
## compact | 12 | 35 | 0 | 47 |
## | 3.649 | 8.828 | 5.021 | |
## | 0.255 | 0.745 | 0.000 | 0.201 |
## | 0.117 | 0.330 | 0.000 | |
## | 0.051 | 0.150 | 0.000 | |
## -------------|-----------|-----------|-----------|-----------|
## midsize | 3 | 38 | 0 | 41 |
## | 12.546 | 20.321 | 4.380 | |
## | 0.073 | 0.927 | 0.000 | 0.175 |
## | 0.029 | 0.358 | 0.000 | |
## | 0.013 | 0.162 | 0.000 | |
## -------------|-----------|-----------|-----------|-----------|
## minivan | 0 | 11 | 0 | 11 |
## | 4.842 | 7.266 | 1.175 | |
## | 0.000 | 1.000 | 0.000 | 0.047 |
## | 0.000 | 0.104 | 0.000 | |
## | 0.000 | 0.047 | 0.000 | |
## -------------|-----------|-----------|-----------|-----------|
## pickup | 33 | 0 | 0 | 33 |
## | 23.497 | 14.949 | 3.526 | |
## | 1.000 | 0.000 | 0.000 | 0.141 |
## | 0.320 | 0.000 | 0.000 | |
## | 0.141 | 0.000 | 0.000 | |
## -------------|-----------|-----------|-----------|-----------|
## subcompact | 4 | 22 | 9 | 35 |
## | 8.445 | 2.382 | 7.401 | |
## | 0.114 | 0.629 | 0.257 | 0.150 |
## | 0.039 | 0.208 | 0.360 | |
## | 0.017 | 0.094 | 0.038 | |
## -------------|-----------|-----------|-----------|-----------|
## suv | 51 | 0 | 11 | 62 |
## | 20.598 | 28.085 | 2.891 | |
## | 0.823 | 0.000 | 0.177 | 0.265 |
## | 0.495 | 0.000 | 0.440 | |
## | 0.218 | 0.000 | 0.047 | |
## -------------|-----------|-----------|-----------|-----------|
## Column Total | 103 | 106 | 25 | 234 |
## | 0.440 | 0.453 | 0.107 | |
## -------------|-----------|-----------|-----------|-----------|
##
## De kruistabel die we nu hebben bevat heel veel informatie, met de toevoegingen prop.r =,prop.c = en prop.t = kan je aangeven of je de rijproporties, colomproporties en de totale proporties wilt weergeven in de kruistabel. Daarbij kan ook de Chi-kwadraattoets toegevoegd worden aan de kruistabel, dit kan met chisq =. De Chi-kwadraattoets wordt onderaan weergeven.
## Warning in chisq.test(t, correct = FALSE, ...): Chi-squared approximation may
## be incorrect##
##
## Cell Contents
## |-------------------------|
## | N |
## | Chi-square contribution |
## |-------------------------|
##
##
## Total Observations in Table: 234
##
##
## | mpg$drv
## mpg$class | 4 | f | r | Row Total |
## -------------|-----------|-----------|-----------|-----------|
## 2seater | 0 | 0 | 5 | 5 |
## | 2.201 | 2.265 | 37.334 | |
## -------------|-----------|-----------|-----------|-----------|
## compact | 12 | 35 | 0 | 47 |
## | 3.649 | 8.828 | 5.021 | |
## -------------|-----------|-----------|-----------|-----------|
## midsize | 3 | 38 | 0 | 41 |
## | 12.546 | 20.321 | 4.380 | |
## -------------|-----------|-----------|-----------|-----------|
## minivan | 0 | 11 | 0 | 11 |
## | 4.842 | 7.266 | 1.175 | |
## -------------|-----------|-----------|-----------|-----------|
## pickup | 33 | 0 | 0 | 33 |
## | 23.497 | 14.949 | 3.526 | |
## -------------|-----------|-----------|-----------|-----------|
## subcompact | 4 | 22 | 9 | 35 |
## | 8.445 | 2.382 | 7.401 | |
## -------------|-----------|-----------|-----------|-----------|
## suv | 51 | 0 | 11 | 62 |
## | 20.598 | 28.085 | 2.891 | |
## -------------|-----------|-----------|-----------|-----------|
## Column Total | 103 | 106 | 25 | 234 |
## -------------|-----------|-----------|-----------|-----------|
##
##
## Statistics for All Table Factors
##
##
## Pearson's Chi-squared test
## ------------------------------------------------------------
## Chi^2 = 221.6011 d.f. = 12 p = 1.104881e-40
##
##
## 6.4 Correlatie
6.4.1 Pearson correlatie
Om de Pearson correlatie tussen twee variabelen uit te rekenen in R moet er sprake zijn van twee continue variabelen waarvoor er geen missende waarden zijn. Als er wel missende waarden in de kolom van de variabele staan, zal R een foutmelding geven. Het berekenen van de correlatie kan met de code cor().
## [1] -0.8057714Het toetsen van de correlatie kan met de code cor.test(). Voor het toetsen van een correlatie met twee continue variabelen maak je gebruik van method= c("pearson").
##
## Pearson's product-moment correlation
##
## data: mpg$cyl and mpg$cty
## t = -20.724, df = 232, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.8465387 -0.7556076
## sample estimates:
## cor
## -0.8057714Wanneer je de correlatie tussen alle variabelen in een dataset wilt uitrekenen, is het ook mogelijk om binnen de haakjes van cor() de naam van de dataset te plaatsen.
6.4.2 Correlatie via ANOVA
De correlatie tussen een continue en een categorische variabele kan berekend worden via de \(R^2\) van een ANOVA tabel. In het onderstaande voorbeeld is de correlatie tussen hwy en class berekend. De code bestaat uit verschillende onderdelen, namelijk het maken van de ANOVA tabel, daar de \(R^2\) van te pakken en daar de wortel van te berekenen. Let op: de correlatie via ANOVA zal altijd positief zijn, kijk dus zelf wat de richting van de correlatie is.
## [1] 0.82939986.4.3 Cramer’s V
De Cramer’s V wordt gebruikt voor het berekenen van een correlatie tussen twee categorische variabelen. Het berekenen van de Cramer’s V kan met het package vcd. In het onderstaande voorbeeld is de Cramer’s V tussen drv en class berekend.
## [1] 0.68811826.4.4 Partiële correlatie
Met het package ppcor kan een overzicht gemaakt worden van de partiële correlaties in de dataset. Voor het voorbeeld willen we de partiële correlaties tussen de variabelen hwy, cyl en cty. De gevonden correlaties zijn gecontroleerd voor de andere variabelen in het model. LET OP ppcor overschrijft de select-functie uit tidyverse. Als je deze wilt gebruiken, moet tidyverse nog geladen worden na het laden van ppcor. Wanneer er een foutmelding voor de functie select blijft, moet je de functie dplyr::select erbij gebruiken zoals ook gedaan is in het voorbeeld hieronder.
## $estimate
## hwy cyl cty
## hwy 1.00000000 0.04794292 0.8915860
## cyl 0.04794292 1.00000000 -0.4072204
## cty 0.89158600 -0.40722036 1.0000000
##
## $p.value
## hwy cyl cty
## hwy 0.000000e+00 4.664299e-01 1.971501e-81
## cyl 4.664299e-01 0.000000e+00 1.013703e-10
## cty 1.971501e-81 1.013703e-10 0.000000e+00
##
## $statistic
## hwy cyl cty
## hwy 0.0000000 0.7295082 29.923576
## cyl 0.7295082 0.0000000 -6.776537
## cty 29.9235758 -6.7765366 0.000000
##
## $n
## [1] 234
##
## $gp
## [1] 1
##
## $method
## [1] "pearson"