Chapter 10 Regressie

In een regressieanalyse draait het om de vraag hoe goed de score van een afhankelijke (te verklaren) variabele voorspeld kan worden aan de hand van één of meerdere onafhankelijke (verklarende) variabelen. De samenhang tussen de afhankelijke en de onafhankelijke variabele(n) wordt gemodelleerd met een lineair model. Hierin wordt de afhankelijke variabele y geschreven als een lineaire combinatie van de onafhankelijke variabele(n) x en een foutenterm \(\epsilon\). In het geval van één onafhankelijke variabele is de regressievergelijking \(y_{i} = \beta_{0} + \beta_{1}x_{i}+ \epsilon_{i}\), waarbij wordt verondersteld dat de foutenterm (error) normaal verdeeld is met gemiddelde 0 en standaarddeviatie \(\sigma\). De regressiecoëfficiënten \(\beta_{0}\) (de constante of ‘intercept’) en \(\beta_{1}\) (de helling of ‘slope’), en de standaarddeviatie \(\sigma\) zijn onbekend en worden geschat met de data.

Voor de voorbeelden over lineaire regressie maken we gebruik van de dataset diamonds die standaard in tidyverse zit.

library(tidyverse)

10.1 Het regressiemodel

Bij regressieanalyse wordt een afhankelijke variabele voorspeld vanuit één of meer onafhankelijke variabelen. Lineaire regressie gaat via lm(), wat staat voor linear model.

Voor de regressieanalyses is het handig om het model op te slaan als object. We gaan nu de prijs van een diamand voorspellen vanuit het gewicht van de diamand. Bij lm() geef je de afhankelijke variabele, de onafhankelijke variabele en de dataset aan. De onafhankelijke variabele volgt altijd na een ~ na de afhankelijke variabele. Wanneer je meerdere onafhankelijke variabelen hebt, volgen deze elkaar met een +.

model1 <- (lm(price ~ carat, data= diamonds))

Nu we de regressieanalyse hebben uitgevoerd en het model hebben opgeslagen in het object model1 kunnen we de regressie output bekijken via summary().

summary (model1)

## 
## Call:
## lm(formula = price ~ carat, data = diamonds)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -18585.3   -804.8    -18.9    537.4  12731.7 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -2256.36      13.06  -172.8   <2e-16 ***
## carat        7756.43      14.07   551.4   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1549 on 53938 degrees of freedom
## Multiple R-squared:  0.8493, Adjusted R-squared:  0.8493 
## F-statistic: 3.041e+05 on 1 and 53938 DF,  p-value: < 2.2e-16

We hebben de analyse nu uitgevoerd, de output bevat de volgende zaken:

Call: hier wordt de code van de uitgevoerde analyse weergeven.
Residuals: hier wordt een samenvatting van de verdeling van de residuen weergeven.
Coefficients: voor de onafhankelijke variabelen wordt in de output de regressiecoëfficiënt, de standaardfout, de t-waarde en tweezijdige overschrijdingskans voor het toetsen of de coëfficiënt van nul verschilt weergeven.
Verder geeft de output de geschatte standaarddeviatie van de residuen (Residual standard error) met bijbehorende vrijheidsgraden (degrees of freedom), het percentage verklaarde variantie (Multiple R-squared), de gecorrigeerde \(R^{2}\) (Adjusted R-squared) en de F-toets die toetst of er een significante stijging in \(R^{2}\) is tenopzichte van het lege model (toets of \(R^{2}\) significant van 0 verschilt)

Vanuit de output kan herleid worden dat het model om de prijs te van een diamant te bepalen vanuit het gewicht van de diamand er als volgt uitziet: \(Price = -2256.36 + 7756.43*carat\).’

Als voorbeeld voor multipele regressie zullen we de lengte van de diamand (in mm) meenemen voor het schatten van de prijs van de diamand, deze variabele heet x. Dit model zullen we opslaan in object model2.

model2 <- (lm(price ~ carat + x, data= diamonds))

In de uitkomsten zien we dat de informatie die gegeven wordt bij deze analyse gelijk is als de informatie bij enkelvoudige regressie. Ook is te zien dat bij coëfficiënts nu, naast de constante, twee variabelen staan. Dit zijn de twee onafhankelijke variabelen die toegevoegd zijn in het model voor het schatten van de afhankelijke variabele price. Beide variabelen hebben een eigen helling, inclusief een toets voor de helling. Het regressiemodel van de onderstaande analyse ziet er alsvolgt uit: \(Price = 1737.95 + 10125.99*carat - 1026.86*x\).

summary (model2)

## 
## Call:
## lm(formula = price ~ carat + x, data = diamonds)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -23422.7   -653.6    -14.2    370.9  12978.4 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1737.95     103.62   16.77   <2e-16 ***
## carat       10125.99      62.55  161.88   <2e-16 ***
## x           -1026.86      26.43  -38.85   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1527 on 53937 degrees of freedom
## Multiple R-squared:  0.8534, Adjusted R-squared:  0.8534 
## F-statistic: 1.57e+05 on 2 and 53937 DF,  p-value: < 2.2e-16

10.1.1 Betrouwbaarheidsinterval voor regressiecoëfficienten

Het berekenen van de betrouwbaarheidsintervallen van regressiecoëfficieënten kan met de code confint(). In deze code moeten het regressiemodel en het betrouwbaarheidsniveau opgegeven worden.

confint(model1, level = 0.95)

##                 2.5 %    97.5 %
## (Intercept) -2281.949 -2230.772
## carat        7728.855  7783.996

10.1.2 Gestandaardiseerde regressiecoëfficiënt beta.

Gestandaardiseerde regressiecoëfficiënten worden ook wel beta benoemd. Door middel van gestandaardiseerde regressiecoëffiënten kunnen effecten van onafhankelijke variabelen onderling met elkaar vergeleken worden. Het berekenen van een beta, kan met het package lm.beta en met de functie lm.beta().

library(lm.beta)

lm.beta(model2)

## 
## Call:
## lm(formula = price ~ carat + x, data = diamonds)
## 
## Standardized Coefficients::
## (Intercept)       carat           x 
##          NA   1.2031344  -0.2887342

Ook is het mogelijk om meteen de lm() functie binnen de lm.beta() code te gebruiken, dan hoef je niet eerst het model op te slaan in een los object.

lm.beta(lm(price ~ carat + x, data= diamonds))

## 
## Call:
## lm(formula = price ~ carat + x, data = diamonds)
## 
## Standardized Coefficients::
## (Intercept)       carat           x 
##          NA   1.2031344  -0.2887342

10.2 Voorspelde waarden en residuen

10.2.1 Voorspelde waarden

Voorspelde waarden komen voort uit een geschat regressiemodel. Nadat je een model opgesteld hebt waarin je y kan voorspellen uit x, kan je door verschillende waarden in te vullen bij x een voorspelde y waarde berekenen. Het opslaan van de voorspelde waarden kan met mutate().

In het volgende voorbeeld zullen we de voorspelde scores van de prijs van diamanten, voorspeld vanuit het gewicht, opslaan als variabele in de dataset. Hiervoor maken we gebruik van het eerder opgestelde regressiemodel. We slaan de informatie op in de nieuwe variabele pred_price (pred van predicted).

diamonds <- diamonds %>%
  mutate(pred_price = (-2256.36 + 7756.43*carat))

Het berekenen van de voorspelde waarden kan ook met de code predict(). Hiervoor maken we gebruik van het object model1 die we eerder gemaakt hebben.

diamonds <- diamonds %>%
  mutate(pred_price2 = predict(model1))

10.2.2 Residuen

Het opslaan van de residuen, of te wel het verschil tussen de voorspelde score en de daadwerkelijke score, kan ook berekend worden met mutate(). We gaan nu de residuen voor het voorspellen van de prijs van een diamand door middel van het gewicht van een diamand opslaan in een nieuwe variabele in de dataset.

diamonds <- diamonds %>%
  mutate(resid_price = price - pred_price)

Het berekenen van de residuen kan ook met de functie resid(), daarbij maken we weer gebruik van het object model1, welke we eerder hebben gemaakt.

diamonds <- diamonds %>%
  mutate (resid_price = resid (model1))

Gestandaardiseerde residuen kunnen op een aantal manieren worden uitgerekend. De beste manier is met de functie studres() van de MASS package. De residuen die je zo uitrekent worden ook wel de gestudentizeerde residuen genoemd binnen regressieanalyse. Een andere manier is met de functie rstandard(). Deze laatste zijn iets anders omdat in de standaardisatie een andere geschatte standaarddeviatie wordt gebruikt.

library(MASS)

diamonds <- diamonds %>%
  mutate (studresid_price = studres(model1))

diamonds <- diamonds %>%
  mutate (stanresid_price = rstandard (model1))

10.3 ANOVA en de F-toets

Om de variantie te analyseren wordt er gebruik gemaakt van ANOVA (analyse of variance) tabellen. ANOVA tabellen verdelen de variantie in een gedeelte dat door het model verklaard kan worden en een deel dat onverklaard blijft (het residu). Het maken van een ANOVA tabel kan met de code anova().

We zullen nu een ANOVA tabel maken bij het model dat de prijs van een diamant schat vanuit het gewicht van de diamant, welke we hebben opgeslagen in model1.

anova (model1)

## Analysis of Variance Table
## 
## Response: price
##              Df     Sum Sq    Mean Sq F value    Pr(>F)    
## carat         1 7.2913e+11 7.2913e+11  304051 < 2.2e-16 ***
## Residuals 53938 1.2935e+11 2.3980e+06                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

In de output is achter de naam van de variabele, in dit geval carat, het deel van de variantie dat verklaard wordt door die variabele weergeven. Achter residuals is het onverklaarde gedeelte van de variantie weergeven. Het is ook mogelijk om ANOVA tabellen te maken bij een multipel regressiemodel. Bij een multipele regressie wordt de verklaarde variantie verdeeld per onafhankelijke variabele. Hierbij geeft de eerste variabele de verklaarde variantie ten opzichte van het lege model. Vanaf de tweede variabele wordt de variantie die extra verklaard wordt ten opzichte van het vorige model weergeven. We maken hierbij gebruik van het object model2 met price als afhankelijke variabele en carat en x als onafhankelijke variabelen.

anova (model2)

## Analysis of Variance Table
## 
## Response: price
##              Df     Sum Sq    Mean Sq  F value    Pr(>F)    
## carat         1 7.2913e+11 7.2913e+11 312552.4 < 2.2e-16 ***
## x             1 3.5206e+09 3.5206e+09   1509.1 < 2.2e-16 ***
## Residuals 53937 1.2583e+11 2.3328e+06                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

In deze output staat achter carat de verklaarde variantie in price door alleen catat. Achter x staat de verklaarde variantie door x bovenop dat deel verklaard door carat (dus wat geeft x aan extra verklaarde variantie als carat al een deel verklaart). Achter Residuals staat het onverklaarde deel van de variantie.

Wanneer je de verklaarde variantie van een voorspeller wilt, gecontroleerd voor alle andere variabelen in het model, en ook dat deel wat ze gezamenlijk verklaren, kan de functie ols() in het package rms worden gebruikt. Hiermee schat je ook een regressiemodel, en als je daarvan de ANOVA-tabel bepaalt, krijg je de gewenste output. Bij dit package is het niet mogelijk om gebruik te maken van te voren opgeslagen objecten (modellen), maar moet het model wel weer opnieuw worden geschat met de ols() functie.

library (rms)

anova(rms::ols(price ~ carat + x, data= diamonds))

##                 Analysis of Variance          Response: price 
## 
##  Factor     d.f.  Partial SS   MS           F         P     
##  carat          1  61128370227  61128370227  26203.67 <.0001
##  x              1   3520554168   3520554168   1509.14 <.0001
##  REGRESSION     2 732647994287 366323997144 157030.76 <.0001
##  ERROR      53937 125825141230      2332817

Achter carat staat nu de variantie verklaard door carat, gegeven dat x al in het model zit; achter x staat de verklaarde variantie door x gegeven dat carat al in het model zit. De totale verklaarde variantie is weegeven achter REGRESSION. Achter ERROR staat de onverklaarde variantie.

Het vergelijken van modellen kan ook met de functie anova(). Met deze functie kunnen ook partiele F toetsen worden uitgevoerd om te toetsen of het toevoegen van een of meerdere predictoren aan een model een significante stijging van de \(R^{2}\) oplevert. In het onderstaande voorbeeld wordt er gekeken of de variabele x een toevoeging heeft in het verklaren van variantie in price, wanneer de variabele carat al in het model zit. We zien dat de p-waarde lager is dan 0.05, variabele x verklaart naast carat dus ook variantie in price. Anders gezegd is de \(R^{2}\) waarden van model 2 dus hoger dan de \(R^{2}\) van model 1.

anova (model1, model2)

## Analysis of Variance Table
## 
## Model 1: price ~ carat
## Model 2: price ~ carat + x
##   Res.Df        RSS Df  Sum of Sq      F    Pr(>F)    
## 1  53938 1.2935e+11                                   
## 2  53937 1.2583e+11  1 3520554168 1509.1 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Voor een vergelijking van een model met het lege model, moet eerst het lege model geschat worden. Dit kan door op de plek van de onafhankelijke variabelen 1 neer te zetten. Deze 1 staat voor de constante. Vervolgens kan met anova() een model met het lege model vergeleken worden.

model0 <- (lm(price ~ 1, data= diamonds))
summary(model0)

## 
## Call:
## lm(formula = price ~ 1, data = diamonds)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -3607  -2983  -1532   1392  14890 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3932.80      17.18     229   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3989 on 53939 degrees of freedom

anova(model0,model2)

## Analysis of Variance Table
## 
## Model 1: price ~ 1
## Model 2: price ~ carat + x
##   Res.Df        RSS Df  Sum of Sq      F    Pr(>F)    
## 1  53939 8.5847e+11                                   
## 2  53937 1.2583e+11  2 7.3265e+11 157031 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

10.4 Modeldiagnostics

10.4.1 Aannames lineaire regressie

De waarnemingen zijn onafhankelijk van elkaar.
Er bestaat een lineair verband tussen de afhankelijke en onafhankelijke variabele.
De residuen zijn normaal verdeeld met gemiddelde 0 en een onbekende standaarddeviatie σ.
De standaarddeviatie σ moet gelijk zijn voor alle waarden van de onafhankelijke variabele (constante variantie of homoscedasticiteit).

10.4.2 Residual plot

Het spreidingsdiagram met op de y-as de gestandaardiseerde residuen en op de x-as de gestandaardiseerde voorspelde waarden wordt de residual plot genoemd en wordt gebruikt om de aannames lineariteit en constante variantie (homoscedasticiteit) te onderzoeken.

We moeten dus eerst de gestandaardiseerde residuen en gestandaardiseerde voorspelde waarden opslaan.

library(MASS)

diamonds <- diamonds %>%
  mutate (sresid = studres(model2))

diamonds <- diamonds %>% 
  mutate(pred = predict(model2),
         zpred = (pred - mean(pred))/sd(pred))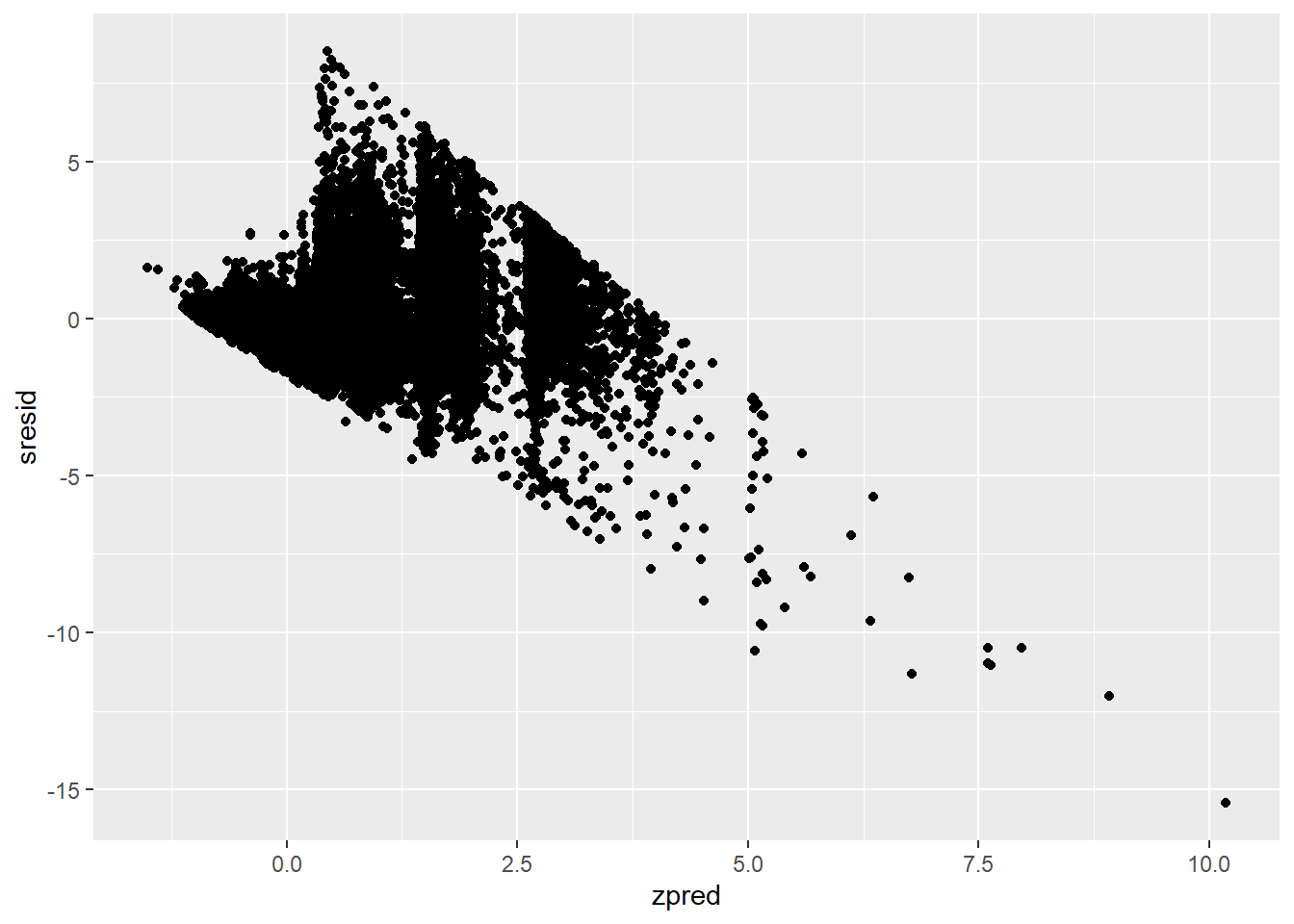

diamonds %>%
  ggplot(mapping = aes(x= zpred, y= sresid)) +
  geom_point()

10.4.3 Partial plot

Een partial plot geeft spreidingsdiagrammen van de gecorrigeerde afhankelijke en een gecorrigeerde onafhankelijke variabele. Beide variabelen zijn gecorrigeerd voor de invloed van de overige onafhankelijke variabelen, waardoor het spreidingsdiagram de unieke samenhang tussen de twee variabelen weergeeft. Voor het maken van de partial plots moet voor iedere grafiek drie stappen doorgelopen worden. We zullen ze nu doorlopen, hierbij gebruiken we het model waarbij de prijs (price) van een diamand wordt voorspeld vanuit het gewicht (carat) en lengte (x) van een diamand.

STAP 1: De eerste stap voor het maken van een partial plot is het berekenen van de residuen van het model waarin je de afhankelijke variabele schat vanuit de onafhankelijke variabele(n) waar je de plot niet voor wilt maken. Deze residuen kunnen gezien worden als ‘de score op price waar het effect van x uit is gehaald’

diamonds$res_price_x <- resid(lm(price ~ x, data = diamonds))

STAP 2: In de tweede stap moet je de residuen berekenen van het model waarin de onafhankelijke variabele waar je de plot wel voor wilt maken geschat wordt vanuit de onafhankelijke variabele(n) waar je de plot niet voor wilt maken.

diamonds$res_carat_x <- resid(lm(carat ~ x, data = diamonds))

STAP 3: In de derde en laatste stap maak je een spreidingsdiagram van de twee residuen variabelen van stap 1 en 2. De residual plot laat de samenhang tussen price en carat zien terwijl er rekening gehouden wordt voor x.

ggplot(data = diamonds,
mapping = aes(y = res_price_x, x = res_carat_x)) +
geom_point(shape = 16, size = 2.5, color = "seagreen") +
geom_smooth(method = lm, se = F, color = "darkgreen") +
ylab("Prijs van de diamand (residual)") +
xlab("gewicht van de diamand (residual)") +
ggtitle("Partial regression plot")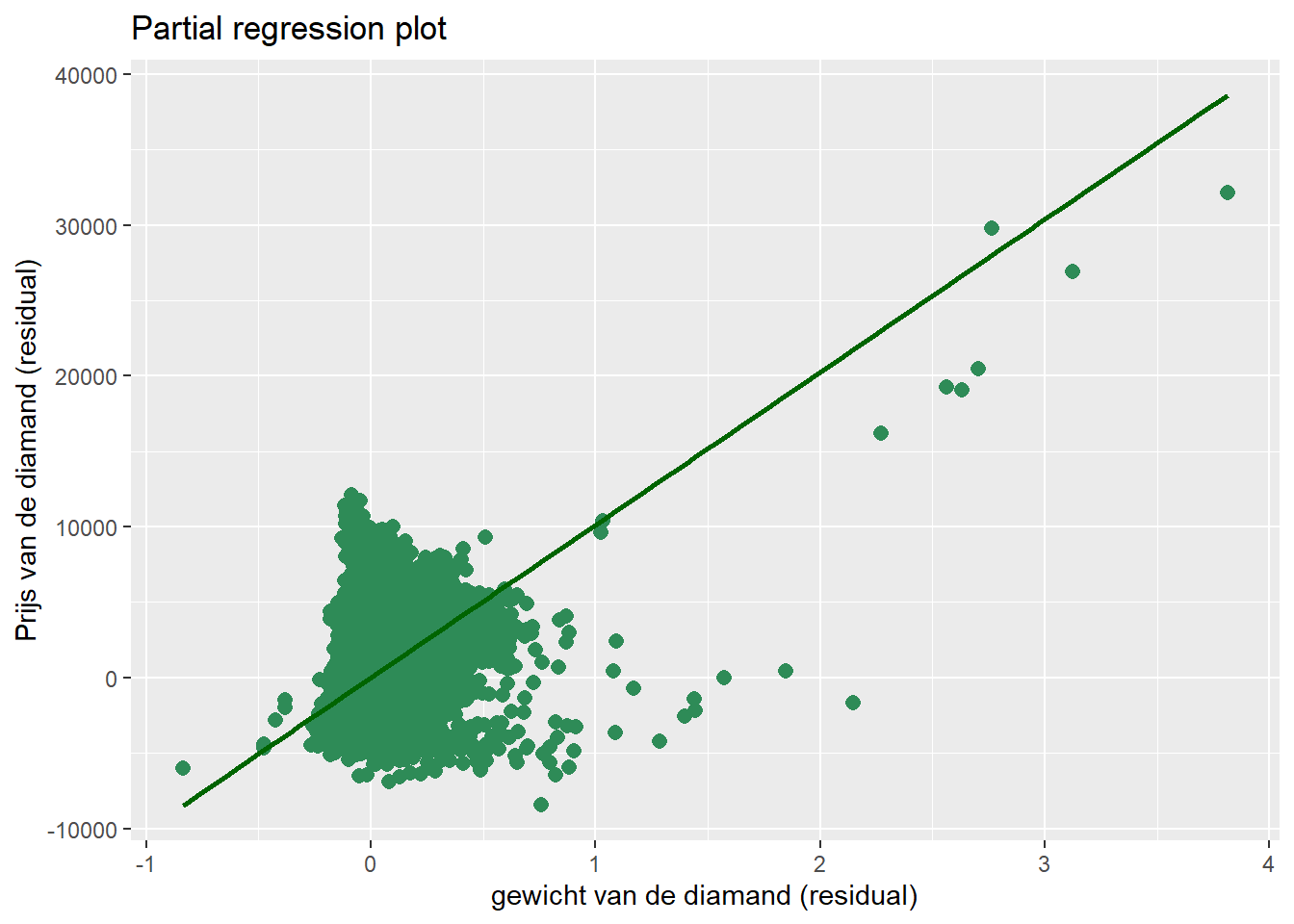

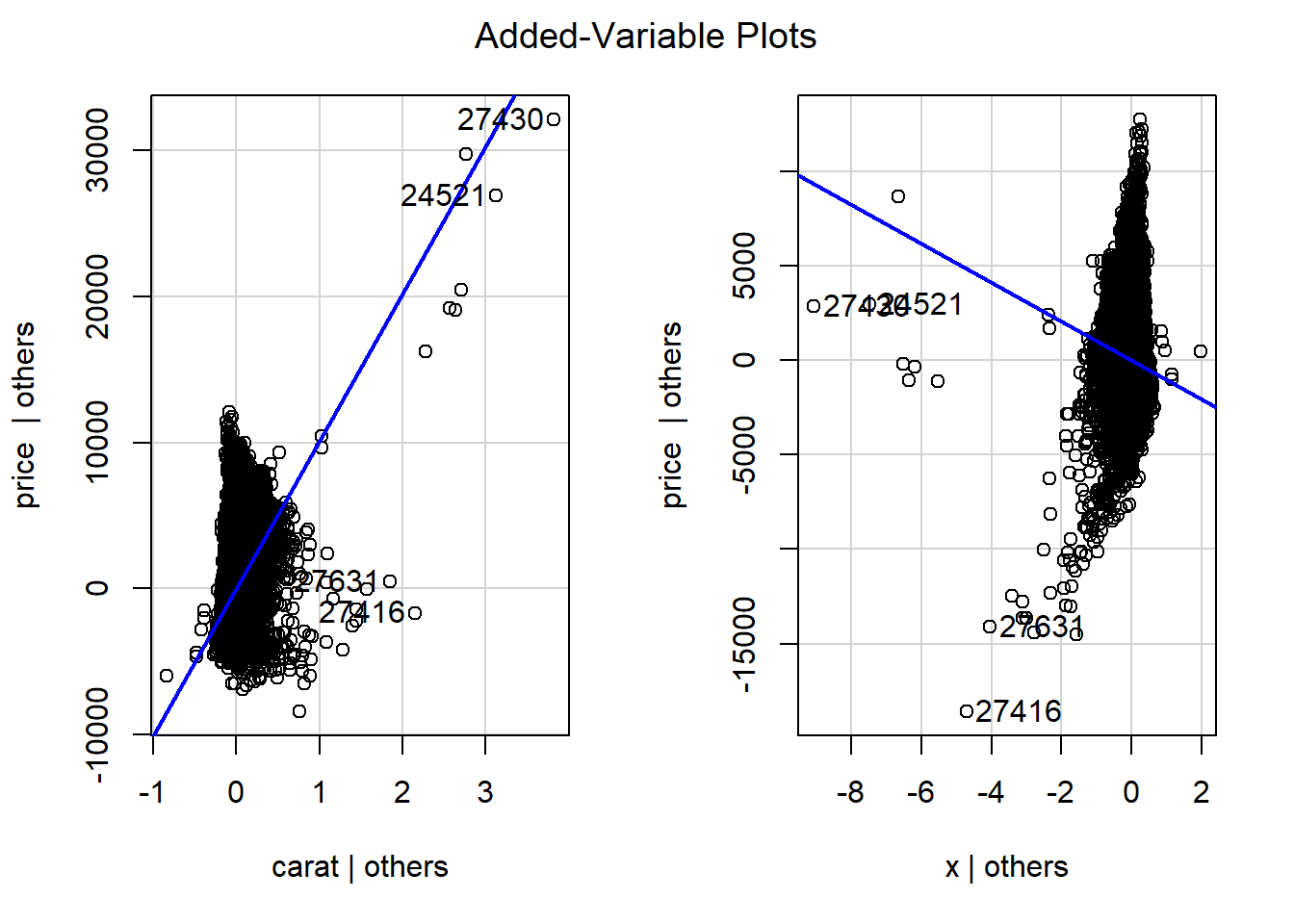
Het maken van een partial regression plot kan ook met de functie avPlots() in het package car.

library(car)

avPlots(model2)

10.4.4 Outliers en invloedrijke punten

Voor het detecteren van outliers en invloedrijke punten kan naast de gestandaardiseerde residuen ook gekeken worden naar de leverage, de Cook’s Distance, de DFFIT en de DFBeta.

hatvalues() ;leverage
cooks.distance() ;Cook’s distance
dffits() ;DFFit
dfbetas() ;DFBeta

Het berekenen en opslaan van de waarden gaat voor elk van de maten op dezelfde manier. Hieronder wordt een voorbeeld weergeven voor het berekenen van de leverage.

diamonds <- diamonds %>%
  mutate (leverage = hatvalues(model1))

10.4.5 VIF-scores

Het berekenen van de VIF-scores kan met de code vif(). Deze code is onderdeel van het rms package.

vif(model2)

##    carat        x 
## 20.32882 20.32882

10.5 Overig

10.5.1 Centreren en interactie aanmaken

Variabelen die in een interactie zitten, moeten gecentreerd worden. Wanneer we een interactie willen tussen de variabelen carat en x, zouden we deze op de volgende manier kunnen maken.

diamonds <- diamonds %>%
  mutate(carat_c = carat - mean(carat),
         x_c = x - mean(x),
         CxX_c = carat_c * x_c)

Het toevoegen van een interactievariabelen in een model kan ook door een : te plaatsen tussen de twee variabelen waar een interactie van gemaakt moet worden.

model3 <- lm(price ~ carat_c + x_c + carat_c:x_c, data = diamonds)
summary(model3)

## 
## Call:
## lm(formula = price ~ carat_c + x_c + carat_c:x_c, data = diamonds)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -26116.3   -633.7    -30.6    341.5  13003.6 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  3739.54      12.41 301.304  < 2e-16 ***
## carat_c      8055.24     128.99  62.448  < 2e-16 ***
## x_c          -279.20      48.54  -5.751  8.9e-09 ***
## carat_c:x_c   372.75      20.33  18.339  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1523 on 53936 degrees of freedom
## Multiple R-squared:  0.8543, Adjusted R-squared:  0.8543 
## F-statistic: 1.055e+05 on 3 and 53936 DF,  p-value: < 2.2e-16