Chapter 11 Variantieanalyse
Variantieanalyse (ANOVA) wordt gebruikt om te onderzoeken in hoeverre gemiddelden in een aantal (vaak meer dan twee) populaties verschillend zijn. De techniek is gebaseerd op het opsplitsen van de variantie van de te onderzoeken variabele in een deel dat kan worden verklaard (toegeschreven aan verschillen in gemiddelden tussen populaties) en een onverklaard deel (verschillen tussen individuen binnen populaties). De techniek wordt ook gebruikt binnen regressieanalyse voor het onderzoeken van de fit van het model: verklaart het model een significant deel van de variantie in de afhankelijke variabele.
ANOVA’s kunnen met verschillende functies en packages uitgevoerd worden. afhankelijk van het gebruiksgemak en output worden enkele functies gebruikt in deze syllabus.
11.1 Eenweg-ANOVA
Een eenweg-variantieanalyse wordt gebruikt om te onderzoeken of de gemiddelden in een aantal populaties (groepen) van elkaar verschillen. Dit kan onder andere met de functie aov(), die we hier gebruiken om te kijken of de price van diamanten verschillend is voor diamanten met een verschillende cut.
Voor het uitvoeren van een eenweg-variantieanalyse is het belangrijk om naar de beschrijvende statistieken van de groepvariabele te kijken. Deze code bestaat uit verschillende stappen, namelijk 1) selecteren van de twee variabelen die je onderzoekt; 2) groepen maken op basis van de variabele cut; 3) het berekenen van gemiddelden en sd etc. van price per groep van cut.
Wegens de gebruikte packages in deze syllabus is de functie dplyr::select gebruikt, meer hierover staat in het hoofdstuk ‘vaak voorkomende fouten’.
Diamonds_samengevat <- diamonds %>%
dplyr::select(price, cut) %>%
group_by(cut) %>%
summarise(Mprice = mean(price), SDprice = sd(price), n = n(),
min = min(price), max = max(price)) %>%
mutate(se = SDprice/sqrt(n),
ci_L = Mprice - qt(0.025, n-1, lower.tail = F)*se,
ci_H = Mprice + qt(0.025, n-1, lower.tail = F)*se
)
Diamonds_samengevat## # A tibble: 5 × 9
## cut Mprice SDprice n min max se ci_L ci_H
## <ord> <dbl> <dbl> <int> <int> <int> <dbl> <dbl> <dbl>
## 1 Fair 4359. 3560. 1610 337 18574 88.7 4185. 4533.
## 2 Good 3929. 3682. 4906 327 18788 52.6 3826. 4032.
## 3 Very Good 3982. 3936. 12082 336 18818 35.8 3912. 4052.
## 4 Premium 4584. 4349. 13791 326 18823 37.0 4512. 4657.
## 5 Ideal 3458. 3808. 21551 326 18806 25.9 3407. 3508.De gegevens kunnen ook grafisch weergeven worden in een meansplot.
Diamonds_samengevat %>%
ggplot(aes(x = cut, y = Mprice))+
geom_errorbar(aes(ymin = (Mprice-se), ymax = (Mprice+se)))+
geom_point(size = 4)+
geom_line()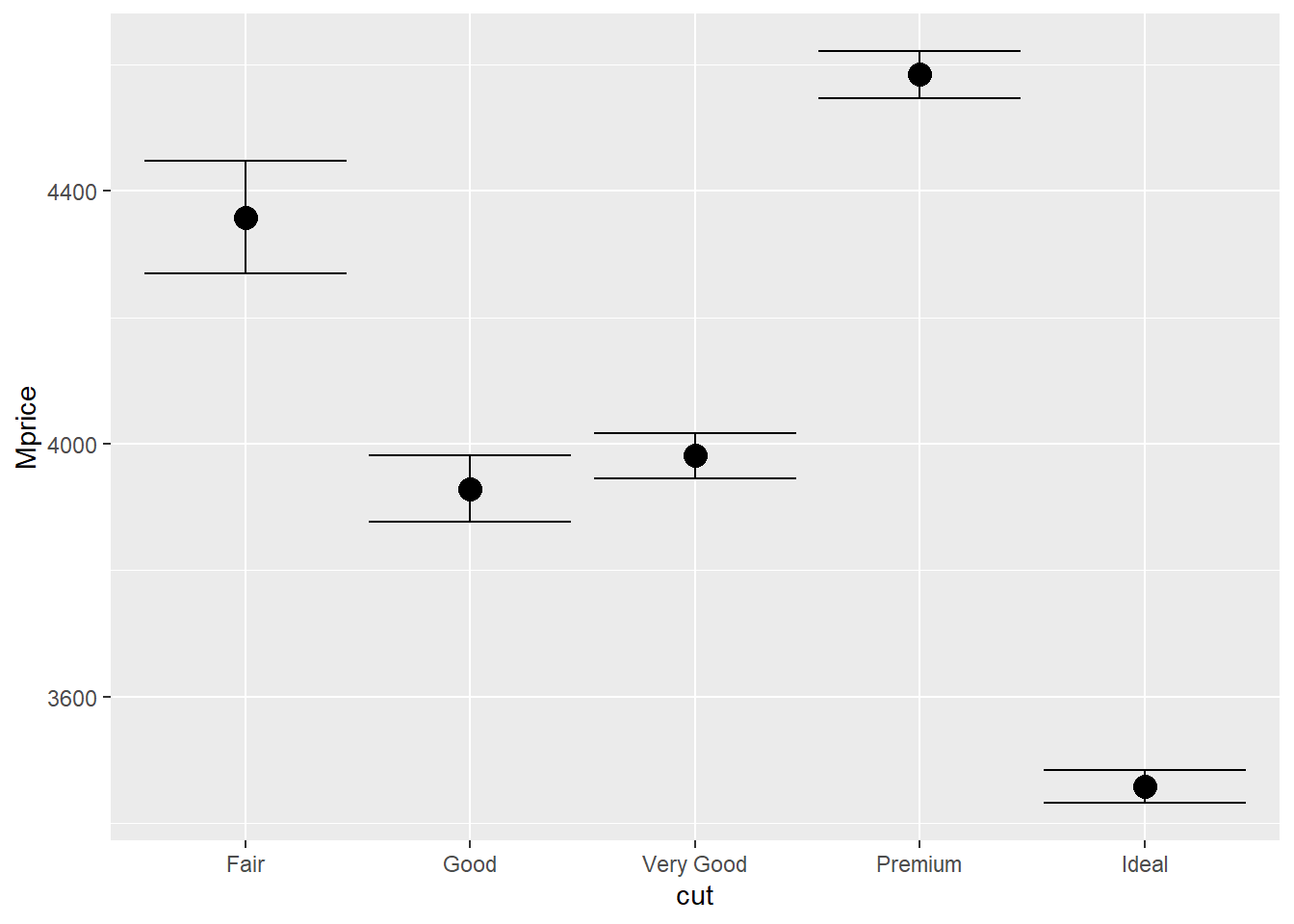
Met de functie summarySE() kunnen de gemiddelden, SE’s en betrouwbaarheidsintervallen in de verschillende groepen uitgerekend worden. Met deze code gebeurt hetzelfde als in de voorgaande code, maar deze code is algemener toepasbaar, dus niet alleen voor eenweg-analyses. Voor het gebruiken van de functie, moet je de functie runnen. De functie heeft drie argumenten (input): de dataset, de uitkomstvariabele
y en de categorische variabele(n) (factoren). Het betrouwbaarheidsniveau van de intervallen is standaard 95%, je kan dit veranderen in bijv. 90% door conf.interval = .90 aan de functie toe te voegen. Binnen deze functie is het mogelijk om meerdere groepsvariabelen toe te voegen, dit is nuttig voor de tweeweg-ANOVA die later behandeld wordt.
summarySE <- function(data=NULL, measurevar, groupvars=NULL, na.rm=FALSE,
conf.interval=.95, .drop=TRUE) {
library(plyr)
# New version of length which can handle NA's: if na.rm==T, don't count them
length2 <- function (x, na.rm=FALSE) {
if (na.rm) sum(!is.na(x))
else length(x)
}
# This does the summary. For each group's data frame, return a vector with N, mean, and sd
datac <- ddply(data, groupvars, .drop=.drop,
.fun = function(xx, col) {
c(N = length2(xx[[col]], na.rm=na.rm),
mean = mean (xx[[col]], na.rm=na.rm),
sd = sd (xx[[col]], na.rm=na.rm)
)
},
measurevar
)
# Rename the "mean" column
datac <- rename(datac, c("mean" = measurevar))
datac$se <- datac$sd / sqrt(datac$N) # Calculate standard error of the mean
# Confidence interval multiplier for standard error
# Calculate t-statistic for confidence interval:
# e.g., if conf.interval is .95, use .975 (above/below), and use df=N-1
ciMult <- qt(conf.interval/2 + .5, datac$N-1)
datac$ci <- datac$se * ciMult
return(datac)
}Tabel_diamonds <- summarySE(diamonds,measurevar = "price", groupvars = "cut")
print (Tabel_diamonds)## cut N price sd se ci
## 1 Fair 1610 4358.758 3560.387 88.73281 174.04403
## 2 Good 4906 3928.864 3681.590 52.56197 103.04499
## 3 Very Good 12082 3981.760 3935.862 35.80721 70.18787
## 4 Premium 13791 4584.258 4349.205 37.03497 72.59358
## 5 Ideal 21551 3457.542 3808.401 25.94233 50.84889De gemiddelden met het 95% betrouwbaarheidsinterval kunnen visueel weergeven worden met de volgende code:
ggplot(Tabel_diamonds, aes(x = cut, y = price, group = 1)) +
geom_errorbar(aes(ymin = price-ci, ymax = price+ci), width = .1) +
geom_line() +
geom_point()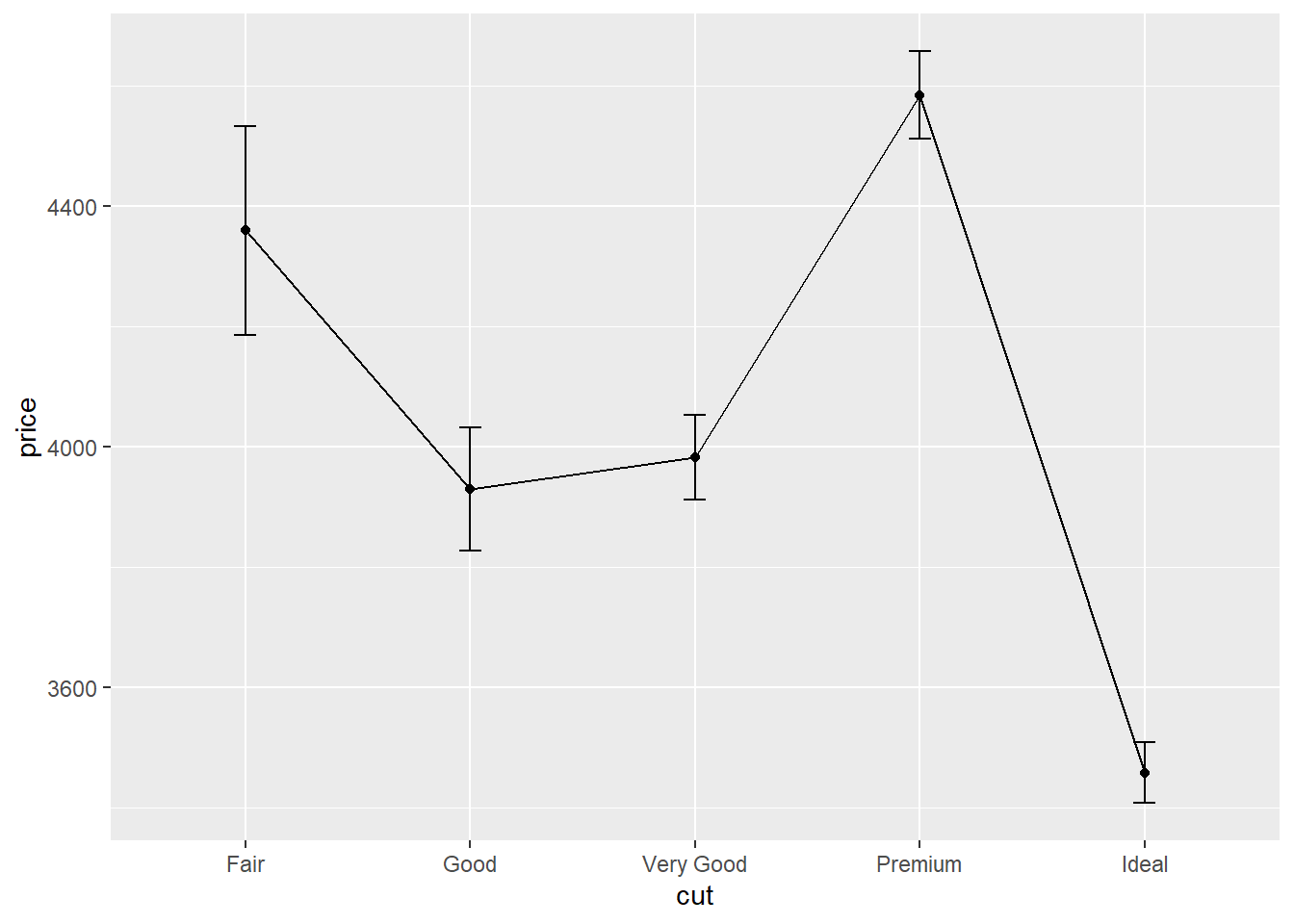
Bij een eenweg-variantieanalyse is één van de aannames dat de varianties in alle groepen gelijk zijn. Voor het uitvoeren van de analyse is het dus goed om dit te controleren. Dit kan als eerste door naar de geschatte SDs in de groepen te kijken. Deze moeten ongeveer even groot zijn; een veel gebruikte vuistregel is dat de grootste niet groter mag zijn dan twee keer de kleinste. Daarnaast kan er ook een toets worden uitgevoerd. Wanneer de groepvariabele meer dan twee groepen heeft, kan hiervoor de code leveneTest() uit het car-package gebruikt worden. Wanneer de onafhankelijke variabele twee groepen heeft, kan de code var.test() gebruikt worden, zoals bij de Independent Samples T Test.
## Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
## group 4 123.6 < 2.2e-16 ***
## 53935
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Hoewel de p-waarde van de Levene toets kleiner is dan 0.05 en de nulhypothese (gelijke populatievarianties) verworpen moet worden, is het verschil tussen SDs niet erg groot (de grootste is 4349.205 en de kleinste is 3560.387; zie output hierboven). De aanname van gelijke populatievarianties is wel geschonden, maar het is een geringe schending en zal geen grote consequenties hebben. Dit is dus niet in lijn met de aannames, dus daar moet rekening mee gehouden worden bij het interpreteren van de resultaten.
Nu we naar de beschrijvende statistieken hebben gekeken en getoetst hebben of de varianties gelijk zijn, kunnen we de eenweg-analyse uitvoeren.
## Df Sum Sq Mean Sq F value Pr(>F)
## cut 4 1.104e+10 2.760e+09 175.7 <2e-16 ***
## Residuals 53935 8.474e+11 1.571e+07
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1De p-waarde is lager dan het significantieniveau 0.05, er zit dus een significant verschil tussen de groepen. We weten echter nu nog niet welke groepen significant van elkaar verschillen. Om daar achter te komen, moeten we een posthoc toets uitvoeren.
De ANOVA kan ook met andere functies en packages worden uitgevoerd. Deze doen dezelfde analyse, maar geven iets andere output. We laten twee voorbeelden zien. Allereerst de functies anova() in combinatie met ols() uit het rms package. Bij het runnen van de code geeft R soms een foutmelding. Wanneer deze foutmelding gegeven wordt, is het belangrijk om eerst de code options(contrasts = c("contr.treatment", "contr.treatment")) te runnen.
options(contrasts = c("contr.treatment", "contr.treatment"))
anova(rms::ols(price ~ cut, data = diamonds))## Analysis of Variance Response: price
##
## Factor d.f. Partial SS MS F P
## cut 4 11041745359 2760436340 175.69 <.0001
## REGRESSION 4 11041745359 2760436340 175.69 <.0001
## ERROR 53935 847431390159 15712087De tweede optie is met de functie Anova() in het car package.
## Anova Table (Type II tests)
##
## Response: price
## Sum Sq Df F value Pr(>F)
## cut 1.1042e+10 4 175.69 < 2.2e-16 ***
## Residuals 8.4743e+11 53935
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 111.1.1 Posthoc toetsen
Met een posthoc toets worden alle groepen individueel met elkaar vergeleken om vast te stellen welke groepen van elkaar verschillen en welke niet. De meest gebruikte posthoc toetsen zullen hier beproken worden
Voor het het analyseren van de groepsgemiddelden is voor dit vak een functie geschreven. Deze functie zit niet in één van de packages van R, maar werkt wel hetzelfde als een package. Indien je de functie wilt gebruiken, moet je de functie in je script hebben staan en gerund hebben. Het is van belang dat de groep variabele als numeriek gezien wordt. De variabele cut is in dit geval een factor, deze zullen we als numeriek gebruiken.
Table.mc <- function(DATMC, UITK, GRP, Bon = F){
GRP <- as.factor(GRP)
n_lev <- length(levels(GRP))
n_test <- n_lev*(n_lev-1)/2
res <- matrix(data = NA, nrow = n_test, ncol = 8)
colnames(res) <- (c("Grp i", "Grp j", "mean dif", "se", "t-value", "p-value", "CI_l", "CI_u"))
i <- 0; j <- 0; t <- 0
for (i in 1:(n_lev-1)){
for (j in (i+1):n_lev){
t <- t + 1
res[t, 1] <- j
res[t, 2] <- i
# diff in mean
m1 <- mean(UITK[which(GRP == i)])
m2 <- mean(UITK[which(GRP == j)])
# mean diff
res[t, 3] <- m2 - m1
mod1 <- lm(UITK ~ GRP, data = DATMC)
anova(mod1)['Residuals', 'Mean Sq']
s <- sqrt(anova(mod1)[2, 3])
n1 <- length(UITK[which(GRP == i)])
n2 <- length(UITK[which(GRP == j)])
# SE diff
se <- s * sqrt(1/n1 + 1/n2)
res[t, 4] <- se
# t-test
res[t, 5] <- (m2-m1)/se
res[t, 6] <- 2*pt(abs((m2-m1)/se), mod1$df.residual, lower.tail = F)
# 95% CI
if(Bon) t_st <- qt(0.025/n_test, mod1$df.residual, lower.tail = F)
else t_st <- qt(0.025, mod1$df.residual, lower.tail = F)
res[t, 7] <- (m2-m1) - t_st * se
res[t, 8] <- (m2-m1) + t_st * se
}
}
return(round(res, 5))
}Nadat je de functie gerund hebt, kun je de code Table.mc() gebruiken. De functie heeft vier argumenten (input): de dataset, de uitkomst variabele
y, de variabele die de groepen aangeeft (een categorische variabele, ook wel factor genoemd) en een indicator die aangeeft of je Bonferroni correctie wilt toepassen of niet. Wanneer je Bon = F gebruikt in de code, wordt de LSD procedure voor post-hoc toetsen gebruikt.
## Grp i Grp j mean dif se t-value p-value CI_l
## [1,] 2 1 -429.89331 113.84940 -3.77598 0.00016 -653.03905
## [2,] 3 1 -376.99787 105.16422 -3.58485 0.00034 -583.12059
## [3,] 4 1 225.49994 104.39521 2.16006 0.03077 20.88450
## [4,] 5 1 -901.21579 102.41155 -8.79994 0.00000 -1101.94325
## [5,] 3 2 52.89544 67.10500 0.78825 0.43055 -78.63089
## [6,] 4 2 655.39325 65.89330 9.94628 0.00000 526.24186
## [7,] 5 2 -471.32248 62.70321 -7.51672 0.00000 -594.22126
## [8,] 4 3 602.49781 49.39387 12.19783 0.00000 505.68544
## [9,] 5 3 -524.21792 45.05019 -11.63631 0.00000 -612.51665
## [10,] 5 4 -1126.71573 43.22459 -26.06654 0.00000 -1211.43628
## CI_u
## [1,] -206.7476
## [2,] -170.8752
## [3,] 430.1154
## [4,] -700.4883
## [5,] 184.4218
## [6,] 784.5446
## [7,] -348.4237
## [8,] 699.3102
## [9,] -435.9192
## [10,] -1041.995211.1.1.1 Bonferroni
De Bonferroni procedure maakt gebruik van gecorrigeerde t-toetsen door aanpassing van het significantieniveau. Deze aanpassing kan aangegeven worden in de functie Table.mc(). Door na Bon = de T van true te zetten, zal de bonferroni correctie toegepast worden.
## Grp i Grp j mean dif se t-value p-value CI_l
## [1,] 2 1 -429.89331 113.84940 -3.77598 0.00016 -749.4856
## [2,] 3 1 -376.99787 105.16422 -3.58485 0.00034 -672.2096
## [3,] 4 1 225.49994 104.39521 2.16006 0.03077 -67.5530
## [4,] 5 1 -901.21579 102.41155 -8.79994 0.00000 -1188.7003
## [5,] 3 2 52.89544 67.10500 0.78825 0.43055 -135.4783
## [6,] 4 2 655.39325 65.89330 9.94628 0.00000 470.4209
## [7,] 5 2 -471.32248 62.70321 -7.51672 0.00000 -647.3397
## [8,] 4 3 602.49781 49.39387 12.19783 0.00000 463.8419
## [9,] 5 3 -524.21792 45.05019 -11.63631 0.00000 -650.6805
## [10,] 5 4 -1126.71573 43.22459 -26.06654 0.00000 -1248.0536
## CI_u
## [1,] -110.30104
## [2,] -81.78619
## [3,] 518.55288
## [4,] -613.73129
## [5,] 241.26919
## [6,] 840.36558
## [7,] -295.30522
## [8,] 741.15377
## [9,] -397.75532
## [10,] -1005.3778511.1.1.2 Tukey
De Tukey procedure maakt gebruik van een aangepaste verdeling en gaat via de code TukeyHSD(). Binnen de code moet je de aov(lm()) functie invullen. Deze functie hebben we eerder al opgeslagen in price.cut.aov (price.cut.oav <- aov(lm(price ~ cut, data = diamonds))).
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = lm(price ~ cut, data = diamonds))
##
## $cut
## diff lwr upr p adj
## Good-Fair -429.89331 -740.44880 -119.3378 0.0014980
## Very Good-Fair -376.99787 -663.86215 -90.1336 0.0031094
## Premium-Fair 225.49994 -59.26664 510.2665 0.1950425
## Ideal-Fair -901.21579 -1180.57139 -621.8602 0.0000000
## Very Good-Good 52.89544 -130.15186 235.9427 0.9341158
## Premium-Good 655.39325 475.65120 835.1353 0.0000000
## Ideal-Good -471.32248 -642.36268 -300.2823 0.0000000
## Premium-Very Good 602.49781 467.76249 737.2331 0.0000000
## Ideal-Very Good -524.21792 -647.10467 -401.3312 0.0000000
## Ideal-Premium -1126.71573 -1244.62267 -1008.8088 0.0000000De resultaten kunnen ook in een plot weergeven worden. In de plot is te zien dat twee betrouwbaarheidsintervallen 0 bevatten, daarbij geldt dat de groepen niet significant van elkaar verschillen.
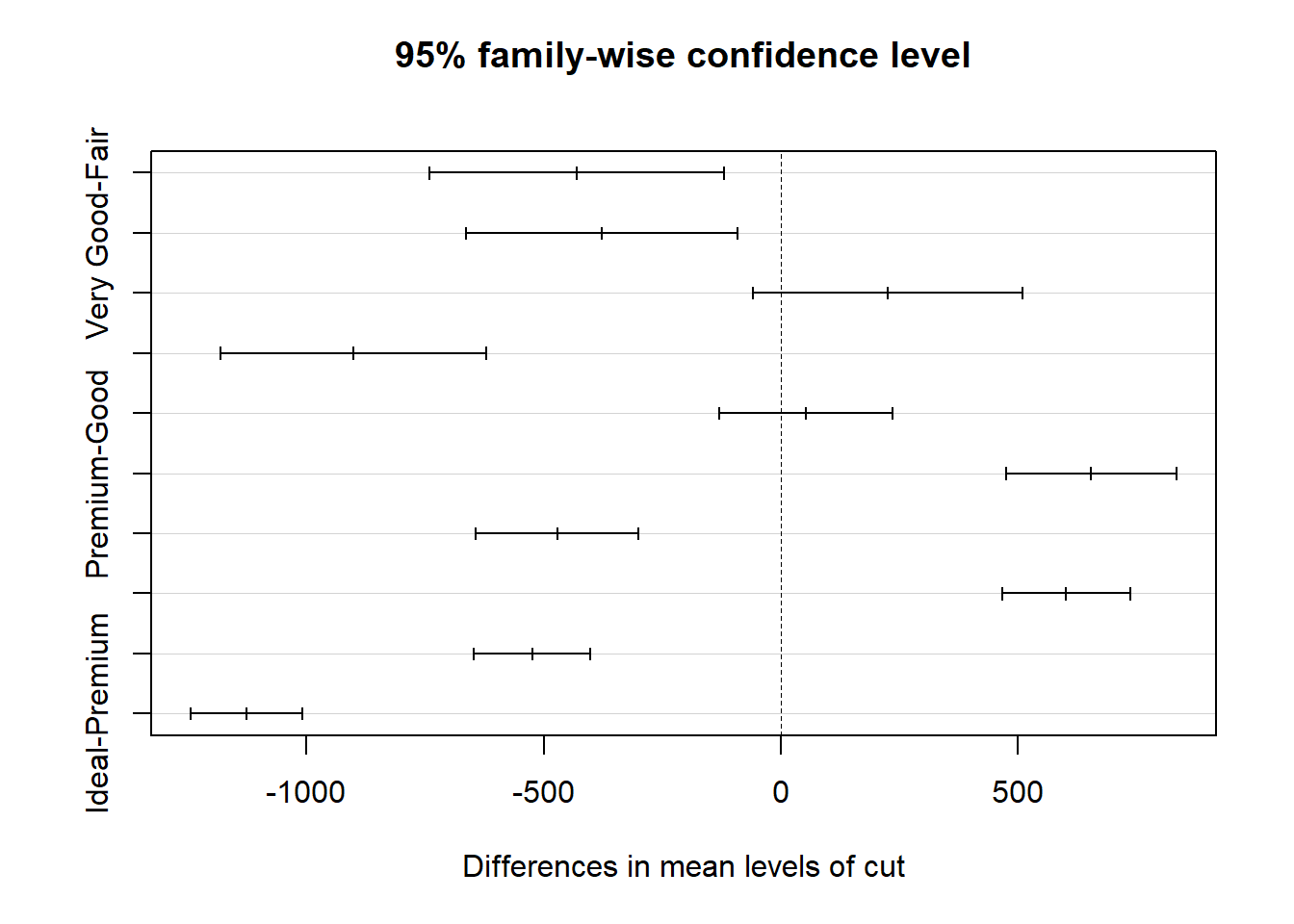
11.2 Tweeweg-ANOVA
We breiden de eenweg-analyse uit door een tweede factor toe te voegen. De tweeweg-analyse gaat ook via de code Anova() uit het car package. Ter illustratie zal er eerst een binaire variabele gemaakt worden van de variabele x, welke de lengte van de diamanten weergeeft. Scores kleiner/gelijk aan de mediaan krijgen score 0, scores groter dan de mediaan krijgen score 1. Vervolgens voeren we een tweeweg-analyse uit met de variabelen cut en x_bin.
## [1] 5.7## Anova Table (Type II tests)
##
## Response: price
## Sum Sq Df F value Pr(>F)
## cut 2.1724e+09 4 66.493 < 2.2e-16 ***
## x_bin 4.0691e+11 1 49818.607 < 2.2e-16 ***
## Residuals 4.4052e+11 53934
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Ook het interactie-effect tussen de twee variabelen kan getoetst worden.
## Anova Table (Type II tests)
##
## Response: price
## Sum Sq Df F value Pr(>F)
## cut 2.1724e+09 4 66.808 < 2.2e-16 ***
## x_bin 4.0691e+11 1 50054.757 < 2.2e-16 ***
## cut:x_bin 2.1108e+09 4 64.915 < 2.2e-16 ***
## Residuals 4.3841e+11 53930
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1De resultaten kunnen ook grafisch weergeven worden. Hiervoor moeten eerst de gemiddelden, SE en betrouwbaarheidsintervallen berekend worden met summarySE().
Tabel_diamonds2 <- summarySE(diamonds,measurevar = "price", groupvars = c("cut","x_bin"))
print (Tabel_diamonds2)## cut x_bin N price sd se ci
## 1 Fair 0 463 1555.330 706.4132 32.829807 64.51425
## 2 Fair 1 1147 5490.394 3624.8661 107.031167 209.99902
## 3 Good 0 2140 1191.442 706.2985 15.267973 29.94162
## 4 Good 1 2766 6046.755 3656.7447 69.529410 136.33482
## 5 Very Good 0 5863 1185.388 742.7898 9.700764 19.01708
## 6 Very Good 1 6219 6618.056 3905.5127 49.524235 97.08462
## 7 Premium 0 5703 1104.270 618.4999 8.190077 16.05566
## 8 Premium 1 8088 7038.062 4174.0958 46.413235 90.98189
## 9 Ideal 0 13017 1192.575 659.3101 5.778755 11.32720
## 10 Ideal 1 8534 6912.320 4025.3780 43.574293 85.41616pd <- position_dodge(0.1) # (0.05 naar links en rechts)
ggplot(Tabel_diamonds2, aes(x = cut, y = price,colour = x_bin, group = x_bin)) +
geom_errorbar(aes(ymin = price-ci,ymax = price+ci), width = .25, position = pd) +
geom_line(position = pd) +
geom_point(position = pd, size = 2)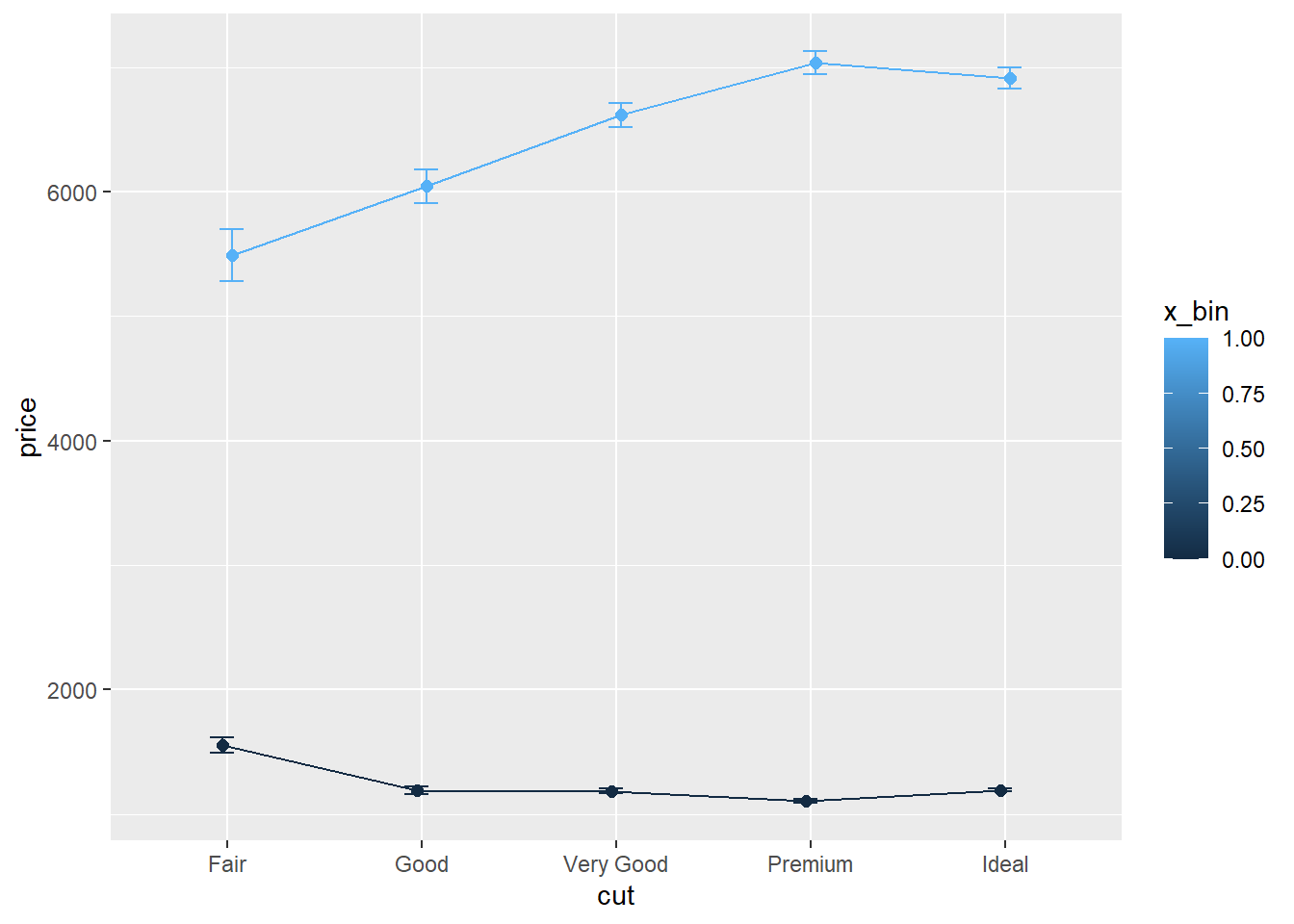
11.3 Ancova
In een covariantieanalyse (ANCOVA) worden naast een afhankelijke variabele en één of meerdere factoren zogenaamde covariaten gebruikt. Dit zijn kwantitatieve variabelen die van invloed zijn op de afhankelijke variabele. Ze maken vaak geen deel uit van het design, en de afhankelijke variabele kan voor hun (verstorende) invloed worden gecontroleerd door de covariaten in de analyse te betrekken. Er wordt dan nagegaan in hoeverre de gecorrigeerde gemiddelden van de afhankelijke variabele verschillen tussen groepen, ofwel, of er een effect is van een bepaalde factor op het gemiddelde van de afhankelijke variabele dat gecorrigeerd is voor de invloed van de covariaten.
Een ancova analyse kan met de functie uit het rms-package. In het onderstaande voorbeeld zullen we kijken naar de prijsverschil tussen de groepen van cut gecorrigeerd voor carat.
## Analysis of Variance Response: price
##
## Factor d.f. Partial SS MS F P
## cut 4 6133201436 1533300359 671.17 <.0001
## carat 1 724218896197 724218896197 317013.48 <.0001
## REGRESSION 5 735260641556 147052128311 64369.36 <.0001
## ERROR 53934 123212493961 2284505In de ANOVA-tabel zien we dat de F-toets van cut significant is. Terwijl er gecontrolelerd wordt voor de variabele carat is er nog een significant verschil tussen de groepen van cut. Naast dat de individuele effecten van de variabelen in het model getoetst worden, wordt ook het gehele model tegen het lege model getoetst. Het resultaat van deze toets staat weergegeven bij REGRESSION.